音と数の関係
どうもこんばんは、学びの森のキノシタです。
もう夏か!というぐらい今日は暑かったですね、、。
<外遊び>の時間に初めてキックベースをしたんですが、今日の暑さに負けないぐらい熱い闘いが繰り広げられました。
その様子はまた後日お伝えするとして…。
今日は<数学の世界>のゼミの様子をお伝えしたいと思います。
タイトルにあるように、今日のテーマは「音楽の数学」でした。
ピアノやヴァイオリンの基準となる音は「ラ」だそうです。
これを弦の振動数で表すと、440Hz。
僕はこれまで、「音」を「数」という切り口から考えたことがなかったので、この段階ですでに衝撃的でした。
まだまだ話は進んでいきます。
次の「ラ」は880Hz、その次の「ラ」は?
440ずつ大きくなっていくから、1320Hz!
ではないんですね…。
なぜならそう考えていくと、基準となる「ラ」のひとつ前の「ラ」は
440Hz-440Hz=0Hz!音が無くなってしまう!!
つまり、基準となる「ラ」から次の「ラ」は、880Hz、1760Hzと2倍に
基準となる「ラ」よりも前の「ラ」は、220Hz、110Hzと1/2倍になっていくということなんです。
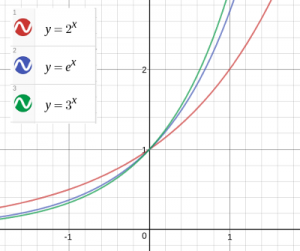
これをグラフに表すと、次のようになります。
そう、指数対数関数のグラフです。
こんな風に「音」と「数(式)」がつながって見えるとは…。またしても、してやられました…。
ここでさらに、
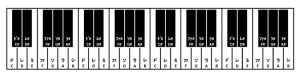
基準の「ラ」から次の「ラ」までを、なぜ「12」の音に分けたのか?
という問いが出されました。
確かに画像を見ると、次の「ラ」までに「12」の音が存在します。
僕はここまででゼミを退席しなければならなかったのですが、生徒に教えてもらったところによると
人類にとって心地の良い音、ハーモニーを奏でるためには、12以外には分けることができないんだとか。
また、その音を使って曲を作る(表現する)際に、12で分けておくのが一番合理的でもあるそうです。
僕はこの話をきいた時、改めて「音」と「数」のつながりから見えてくる、人類の叡智みたいなものを感じました。
この音って心地良いな、と思う音をどうしたらみんなが聴くことができるか?
その音を使って、どうしたらもっとたくさんの表現が生み出せるか?
そんなことを考えながら、「音」と「数」とのつながりをつくっていったのかもしれないと思ったからです。
僕は音楽に苦手意識があるし、自分にはわからないものと位置付けて敬遠してきたところがあります。
でも今回のゼミで、ちょっと感謝の気持ちが湧きました。
最後まで参加してた生徒たちは、どんなことを感じ、考えたのでしょうか。
ブログに書いてもらったりしようかな。レポートみたいな感じで。
あ、ちょっと面白そうなアイデアが浮かんできましたよー!
では、また~