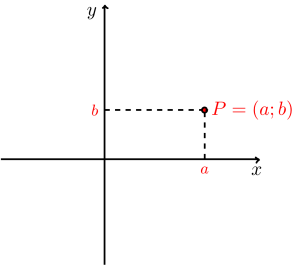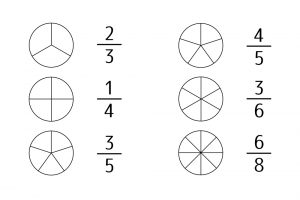分数って何だろう?
こんにちは、学びの森のキノシタです。
今日は<数学の世界>のゼミに参加したので、その様子をお伝えしたいと思います。
今日のテーマは「分数」でした。
皆さんは誰かに「分数ってどんな数?」と聞かれたら、どうこたえますか?
上の数を下の数で割った数?
小数では表すことができない数?
計算しにくいやっかいな数?
数学の世界では、「2つの数を使って1つの数を表した数」であり「等しい数が無限にある数」と考えるそうです。
自然数、例えば「1」と等しい数は「1」以外に存在しません。
小数も「0.1」と等しい数は「0.1」以外に存在しません。
ですが、分数は「1/2」=「2/4」=「3/6」=…というように、等しい数が無限に存在するんです。
だから分数は、他の数とはまったく違う性質を持った数と言えます。
この時点で、僕は目から鱗でした。
なぜなら、自然数や小数、分数が、そもそも「違う」数だという前提が僕にはなかったからです。
でも「違う」という前提で一つひとつの数を見ると、確かに同じところや似てるところ、違うところに目が向くようになります。
そもそもの前提が変わると、今まで持っていた知識と知識のあいだに新しいつながりができました。
・2つの数で1つの数を表している
・等しい数が無限に存在する
このふたつの性質があるから、「分数」は一次関数の「座標」や「傾き」や「直線」と関係がある
ということが、この時初めてしっかりとつながりました。
「座標」は(2.1)のように2つの数で1つの数を表しています。
「傾き」も Xの増加量 と Yの増加量 という2つの数で1つの数を表しています。
そして「直線」は「座標」で表される無限な点の集まりです。
今まで僕はこれ↓
と、これ↓
と、これ↓
は同じものだと思って見えていませんでした。
しかし、つながりができたことによって、同じものに見えるようになりました。
こうした自分の中での変化は、今まででも起こったことがあります。
それはいわば、新しい世界が目の前に広がる経験です。
僕が一番驚いたのは、こうした変化が「分数」によって起こったことでした。
というのも、僕の中で「分数」は「つまらない・難しい・訳が分からない」ものでした。
でもそれは、僕自身が「分数」と向き合う前提となるものを持ち合わせていなかったからにすぎないのかもしれません。
きっと数学には、僕の持ち合わせていなかったたくさんの前提が存在するんだと思います。
その前提を手に入れることで見えてくる新しい世界を、ゼミに参加している生徒も楽しみにしている感じがします。
これから、どんどんその世界をいっしょに見ていきたいと思います。
では、また~